Получение кругового вращающегося магнитного поля

Круговым вращающимся магнитным полем называется поле, вектор результирующей магнитной индукции которого неизменен и вращается с постоянной угловой скоростью. Рассмотрим, как изменяется магнитное поле катушки, по которой протекает переменный ток (рис. 2.1):

                                  

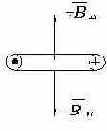
Рис. 2.1. К определению направления вектора НС катушки с переменным током.

Из рис. 2.1 видно, что вектор магнитной индукции

 изменяется по величине от  до , но направление его неизменно.

Рассмотрим, как получить вращающееся магнитное поле в двухфазной электрической сети с помощью двух катушек А и В (рис. 2.2).

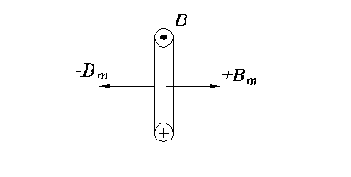
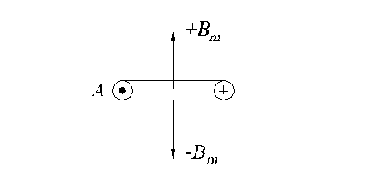
Рис. 2.2. К получению кругового  вращающегося магнитного поля в двухфазной электрической цепи.

Если оси двух катушек

 и , сдвинутые в пространстве относительно друг друга на 90 пространственных градусов, обтекаются токами

                                

;  ,                                                                        (2.1)

то векторы магнитной индукции катушек сдвинуты относительно друг друга также на 90  электрических градусов.

Так как обе катушки совмещены в пространстве, то они создают магнитное поле, модуль вектора результирующей магнитной индукции которого будет равен

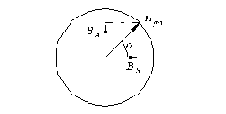
Рис. 2.3. К расчету модуля вектора результирующей магнитной индукции.

 

                                     

;                           (2.2)

                                  

,

отсюда

                                   

.                                                                                  (2.3)

За один период изменения тока двухфазной питающей сети вектор результирующей магнитной индукции сделает один полный оборот:

                                     

.

За одну секунду результирующий вектор магнитной индукции делает

 оборотов, а за 60 с. он сделает

                                   

 .

Вращающееся магнитное поле является круговым при соблюдении следующих условий: сдвиг катушек в пространстве на угол

; сдвиг токов катушек во времени на угол ; равенство магнитодвижущих сил (МДС) обмоток катушек.
Нарушение любого из условий образования кругового вращающегося магнитного поля приводит к образованию эллиптического поля, при котором конец вектора результирующей магнитной индукции описывает не окружность, а эллипс (рис.2.4). В этом случае вектор результирующей магнитной индукции изменяется по амплитуде.

Эллиптическое поле можно представить как сумму двух неравных по амплитуде круговых полей, вращающихся с синхронной частотой  в противоположные стороны.



                 

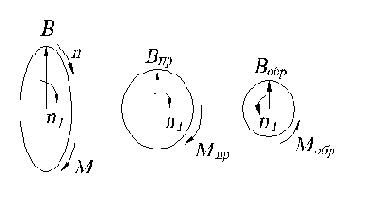
Рис.2.4. Образование эллиптического вращающегося магнитного поля.

Круговое поле , вращающееся в одном направлении с эллиптическим, называется прямым, а второе поле - обратным.

Прямое поле создает вращающий момент двигателя , а обратное – тормозящий момент . С увеличением эллиптичности поля за счет изменения углов сдвигов во времени  и в пространстве  или уменьшении магнитодвижущей силы одной из обмоток статора прямая составляющая поля и момента убывает, а обратная – возрастает. Уменьшение результирующего момента  при неизменном моменте нагрузки приводит к снижению частоты вращения ротора. Когда полностью не выполняется хотя бы одно из условий кругового поля, т. е. , или , или , или , поле статора становится пульсирующим. В этом случае двигатель не развивает вращающего момента при неподвижном роторе. Для объяснения этого явления пульсирующее магнитное поле  можно заменить двумя полями  и , вращающимися в противоположные стороны с синхронной частотой . Амплитуды этих полей равны половине амплитуды пульсирующего поля.

При неподвижном роторе оба поля вращаются относительно ротора с одинаковой частотой и скольжением. Каждое из них наводит в обмотке ротора токи, равные по амплитуде вследствие равенства полей и скольжений. Возникают равные по модулю вращающие моменты  и , направление которых противоположно, как и направление полей. Результирующий момент равен нулю, поэтому ротор не вращается.

Таким образом, изменяя форму поля от пульсирующего через эллиптическое до кругового, можно регулировать вращающий момент от нуля при пульсирующем поле до максимального при круговом.


Соответственно частота вращения ротора будет изменяться от нуля при пульсирующем поле до максимальной при круговом. Способ управления, основанный на изменении амплитуды напряжения управления , называется амплитудным, на изменении угла  - фазовым, на изменении угла  - пространственным. Последний способ применим только для двигателей специальной конструкции, позволяющей поворачивать обмотки возбуждения () и управления () относительно друг друга.

Рассмотрим теперь получение кругового вращающегося магнитного поля в трехфазной электрической цепи.

Возьмем три одинаковые катушки с токами:

.



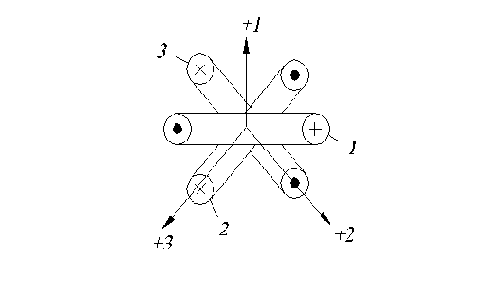
Рис.2.5. К образованию кругового вращающегося магнитного поля в трехфазной цепи.

Положительные направления осей катушек обозначим как . Индукцию первой катушки обозначим , второй-, третьей -. Построим вектор результирующей индукции для моментов времени (рис.2.6).



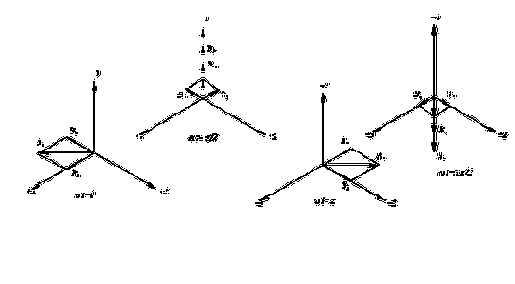
Рис.2.6. Вращение вектора результирующей магнитной индукции.

Вектор результирующей магнитной индукции равен  и вращается с постоянной угловой скоростью  в сторону катушки с отстающим током. Если ток  пропустить по третьей катушке, а ток  по второй, то направление вращения вектора результирующей магнитной индукции изменится на обратное.

Сравним двухфазную (рис.2.7а) и трехфазную (рис.2.7б) электрические цепи.

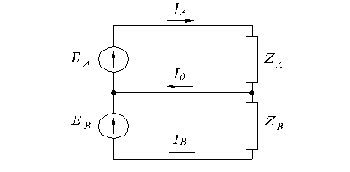
а)







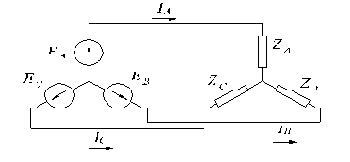
б)



Рис.2.7.  Распределение токов в двухфазной (а) и трехфазной (б) электрических цепях.

При симметричной нагрузке  в двухфазной  и трехфазной системе необходимо иметь три провода. Но в трехфазной системе все три провода обтекаются одинаковым током , а в двухфазной через третий провод протекает ток в  раз больше фазного тока. Поэтому сечение этого провода должно быть больше. Кроме того, магнитная индукция вращающегося магнитного поля в трехфазной системе в 1,5 раза выше. По этим причинам двухфазный ток применяется только в специальной аппаратуре.



2.2. Основные принципы выполнения многофазных обмоток

В электрических машинах переменного тока обмотки размещаются в пазах, расположенных на внутренней поверхности статора и внешней поверхности ротора электрической машины. Проводники обмотки соединяются между собой, образуя ряд катушек. Все катушки одной группы соединяются между собой, образуя одну фазу обмотки. Каждая из фаз обмотки может иметь несколько параллельных ветвей.

Каждый виток обмотки размещается в пазах, находящихся друг от друга на расстоянии, примерно равном одному полюсному делению :

                                        ,                                                                                         (2.4)

где

          D – диаметр внутренней расточки статора;

           p – число пар полюсов.

Если под каждым полюсом расположено только по одной катушке каждой фазы, то такая обмотка называется сосредоточенной. При большем числе катушек под каждым полюсом обмотка называется распределенной.

 

                            а)                                                                     б)



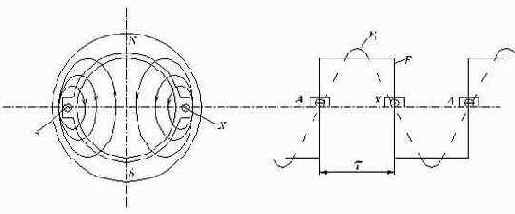
Рис.2.8. Схема двухполюсной машины с сосредоточенной обмоткой (а) и диаграмма распределения ее намагничивающей силы (б).

Намагничивающая сила, создаваемая обмоткой переменного тока, распределена вдоль окружности статора и ротора. Форма кривой ее распределения зависит от типа обмотки. Обычно стремятся, чтобы эта кривая была по возможности близка к синусоиде. При этом ЭДС, индуктируемые в катушках, образующих обмотку статора, будут иметь приблизительно синусоидальную форму, т. е. высшие гармоники в кривой ЭДС будут малы.     

Для этой цели принимают ряд мер: распределение каждой фазы по нескольким пазам, укорочение шага обмотки и скос пазов.

Рассмотрим сначала двухполюсную машину с простейшей сосредоточенной обмоткой, у которой все витки, включенные в фазу , находятся в пазах, расположенных в диаметральной плоскости (рис.2.8а) При протекании тока от начала фазы A к ее концу X возникает двухполюсный магнитный поток.


При максимальном значении тока в катушке намагничивающая сила  будет иметь максимальную величину . При условии равенства нулю магнитных сопротивлений участков магнитопровода распределение намагничивающей силы вдоль окружности статора будет иметь прямоугольную форму (рис.2.8б). Согласно разложению в ряд Фурье прямоугольной формы кривой при сосредоточенной обмотке, отклонение формы поля от синусоидальной велико, поэтому такая обмотка практически не используется.

При питании переменным током однофазной обмотки возникает магнитное поле, пульсирующее во времени с частотой  изменения тока. При синусоидальном распределении намагничивающей силы в каждой точке воздушного зазора, расположенной на расстоянии x от оси обмотки, будет действовать намагничивающая сила (НС), изменяющаяся по закону:

                           ,                                                    (2.5)

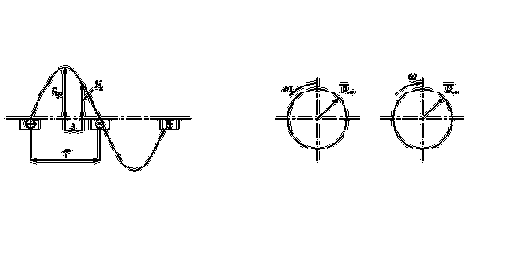
где  - намагничивающая сила в точке, расположенной на оси обмотки (рис.2.9а).

           

	a)		б)		в)

 

                    

Рис.2.9.Диаграмма распределения намагничивающей силы в воздушном зазоре (а) и годографы пространственного вектора МДС (б, в).

Это выражение можно преобразовать к виду:

.                                      (2.6)

Каждый из членов полученного выражения представляет собой вращающуюся или бегущую волну намагничивающей силы. В данном случае образуются две,  вращающиеся в противоположные стороны волны НС: прямая волна , вращающаяся по направлению вращения ротора электрической машины (рис.2.9б), и обратная волна  (рис.2.9в), вращающаяся в противоположном направлении. Следовательно, пульсирующее магнитное поле можно представить в виде двух вращающихся в противоположные стороны магнитных полей, в каждом из которых максимальные значения результирующей НС и результирующей индукции в различные моменты времени остаются неизменными.


Содержание раздела

---

---