Эллиптическое поле

Круговое вращающееся магнитное поле возникает только при симметрии токов, проходящих по катушкам (симметрии НС катушек отдельных фаз), при симметричном расположении этих катушек в пространстве и при сдвиге во времени между фазовыми токами, равном пространственному сдвигу между катушками. При несоблюдении хотя бы одного из этих условий возникает не круговое, а эллиптическое вращающееся поле (рис.2.22а), у которого максимальное значение результирующей индукции для различных моментов времени не остается постоянным, как при круговом поле. В таком поле пространственный вектор НС

 или индукции  описывает эллипс. Эллиптическое поле можно представить в виде

       

                                   а)                                                б)                                      в)

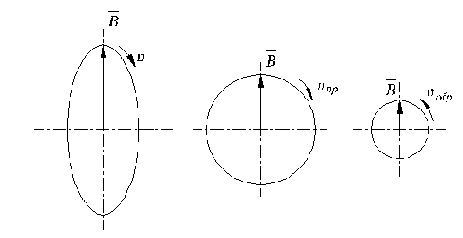
Рис. 2.22. Эллиптическое магнитное поле в рабочем зазоре машины (а) и его разложение на два составляющих круговых поля: прямое (б) и обратное (в).

двух эквивалентных круговых полей, вращающихся в противоположных направлениях рис.2.22б, в). Разложение эллиптического поля на прямое и обратное круговые поля производится методом симметричных составляющих, с помощью которого определяются НС прямой и обратной последовательностей. Рассмотрим, как осуществляется это разложение на примере двухфазной обмотки при питании ее несимметричными токами.

Допустим, что НС

 фазы B-Y опережает НС  фазы A-X на какой-то угол , т. е.

                                                                      (2.33)

причем в общем случае

.

Представим каждый из векторов НС

 и  в виде суммы двух векторов прямой и обратной последовательностей:

                                                                                                     (2.34)

При этом

                                                                                                           (2.35)

Векторы

 и  образуют систему НС

прямой последовательности (рис. 2.23a), причем  опережает  вектор  на угол . Векторы  и  

б)

а)

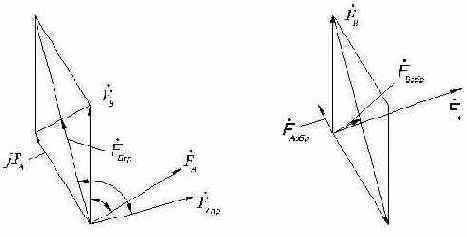
Рис. 2.23. Диаграмма разложения векторов НС двухфазной обмотки на систему векторов прямой (а) и обратной (б) последовательностей.

образуют систему векторов НС обратной последовательности (рис. 2.23б), причем вектор  опережает вектор  на угол .

Величины векторов прямой и обратной последовательностей найдем, подставив последнюю систему в выражения для  и  (2.34):

                                                                       (2.36)

Умножим первое уравнение  системы на :

                                                                                                           (2.37)

Получаем ;  .

Так как

                             ,                                                                       (2.38)

то уравнения бегущей волны для прямого и обратного круговых полей имеют вид:

                                                                (2.39)

При рассмотрении работы многофазных электрических машин, обычно заданными величинами являются напряжения, подводимые к машине, и сопротивления фаз. В общем случае для определения свойств машины требуется разложить на симметричные составляющие подводимые напряжения, по которым затем определяются токи и НС прямой и обратной последовательностей.

Перейдем от системы НС (2.34) к системе токов:

                                                              (2.40)

где

 и  - эффективные числа витков обеих фаз с учетом обмоточных коэффициентов.

Так как  

                                                                       (2.41)

то                                                                   

                                                         (2.42)

где 

.

В каждой из фаз токи прямой и обратной последовательностей создают падения напряжений, сумма которых равна подведенному напряжению:

                                               (2.43)  

где

 - сопротивления фаз A и B для токов прямой и обратной последовательностей.

С учетом выражений  и  (2.42):

                                              (2.44)


Содержание раздела

---

---