Сжимаемость жидкости

Сжимаемость жидкости это свойство жидкостей изменять свой объём при изменении давления.

Сжимаемость характеризуется коэффициентом объёмного сжатия (сжимаемости) ?P, представляющим собой относительное изменение объёма жидкости W при изменении давления P на единицу.

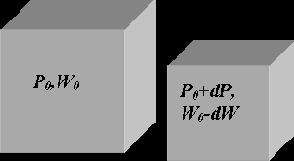
Знак минус в формуле указывает, что при увеличении давления объём жидкости уменьшается.

Единицы измерения: Па-1 (Паскаль. 1Па=1Н/м2).

Перепишем определение

в виде

Обе части умножим на знаменатель и перенесём в левую часть

Учтём, что

и подставим в предыдущее равенство

Выразив отсюда W, можно получить формулу для вычисления нового значения объёма при известном увеличении давления

Если учесть, что все изменения объёма происходят при неизменной массе за счёт изменения плотности (

), можно получить формулу изменения плотности при изменении давления

Откуда выразив ?, получим

Изменение объёма dW, происходящее за счёт изменения плотности d? при постоянной массе, можно записать в виде

Подставив это в определение ?P, определим коэффициент сжимаемости жидкости через изменение плотности

Отсутствие знака минус в этом выражении означает, что увеличение давления приводит к увеличению плотности.

Величина, обратная коэффициенту сжимаемости, или, по-другому, коэффициенту объёмного сжатия

, обозначается

и называется объёмным модулем упругости жидкости.

Тогда предыдущая формула примет вид

Это выражение называется законом Гука для жидкости.

Единицы измерения: [Па], [МПа], [кГс/ см2].

Модуль упругости Еж зависит от температуры и давления. Поэтому различают два модуля упругости: адиабатический и изотермический. Первый имеет место при быстротекущих процессах без теплообмена. Процессы, происходящие в большинстве гидросистем, происходят с теплообменом, поэтому чаще используется изотермический модуль упругости. Примерная форма зависимостей Eж от P и t0 представлена на графиках. Всё это говорит о том, что жидкости не вполне точно следуют закону Гука.

Приведём несколько примеров значений модулей упругости.

Минеральные масла, используемые в технологических машинах с гидравлическим приводом, при t0 = 20 оC имеют объёмные модули упругости 1,35·103 ÷ 1,75·103 МПа (меньшее значение относится к более легкому маслу), бензин и керосин – приблизительно 1,3·103 МПа, глицерин - 4,4·103 МПа, ртуть – в среднем 3,2·103 МПа.

В практике эксплуатации гидравлических систем имеются случаи, когда вследствие действия того или иного возмущения в жидкости может значительно изменяться давление. В таких случаях пренебрежение сжимаемостью приводит к существенным погрешностям.

Известно, что скорость распространения звука с в однородной жидкости можно определить по формуле

Если вспомнить, что

, и подставить это значение в формулу скорости распространения звука, получим

В этом случае изменение плотности жидкости, вызванное изменением давления, будет

Если считать, что жидкость несжимаемая, т.е. dr = 0, то окажется, что скорость распространения звука в жидкости по приведённой формуле окажется бесконечной (c = ¥). При использовании такого значения c в случае достаточно больших объёмов жидкости (озеро или нефтепровод) или быстрого изменения давления, например, при резком закрытии или открытия запорного устройства в трубопроводе, результаты расчётов окажутся существенно неточными. По этой причине в описанных условиях принимать жидкость несжимаемой недопустимо.

Содержание раздела

Главная сайта