Скорость распространения гидравлической ударной волны в трубопроводе

Изменения давления и скорости потока в трубопроводах происходят не мгновенно в связи с упругостью твёрдых стенок трубы и сжимаемостью рабочей среды, а с некоторой конечной скоростью, обусловленной необходимостью компенсации упругих деформаций жидкости и трубы. Рассмотрим случай когда в трубопроводе длиной L и площадью сечения ? под давлением Р находится жидкость, плотность которой ?. Предположим, что в момент времени t в сечении 1 – 1 давление повысится на величину dp. Это повышение вызывает увеличение плотности на величину d?, а также расширение внутреннего диаметра трубы. Следовательно, площадь проходного сечения увеличится на величину d?. В результате увеличится объём W участка трубы на величину dW. За счёт этого произойдет увеличение массы жидкости находящейся в трубе на участке длиной L. Масса увеличится за счёт увеличения, во-первых, плотности жидкости, во-вторых, за счёт увеличения объёма W.

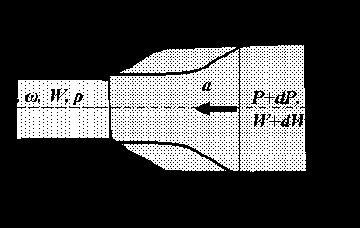
Такая ситуация рассматривалась при выводе уравнения неразрывности потока в дифференциальной форме, с той только разницей, что там рассматривалось лишь изменение массы во времени, без учёта вызвавших это изменение причин

. По аналогии с приведённым уравнением запишем выражение, описывающее изменение массы за счёт изменения давления

Жидкость под действием указанного повышения давления устремится с некоторой скоростью а в слои с меньшим давлением, в которых также будет повышаться плотность и увеличиваться напряжение в стенках трубопровода, способствующее увеличению площади трубопровода. В связи с этим потребуется некоторое время на распространение этих деформаций вдоль трубопровода.

С другой стороны, перемещение массы dm за время dt происходит под влиянием результирующей Fр сил давления, действующих вдоль линии движения на торцовые поверхности цилиндрического объёма длиной L

В этом случае уравнение импульса силы может быть представлено в следующем виде

Отсюда

Имея в виду, что

, и подставив это в предыдущее выражение, получим

Заметим, что произведение

Приравняем оба выражения для

и получим:

.

Выразим из последнего равенства величину a2

Разделим числитель и знаменатель на W, а первое слагаемое в знаменателе искусственно умножим и разделим на ?:

.

Обратим внимание на то, что

. После подстановки этих равенств в последнее выражение и извлечения корня получим выражение для скорости распространения ударной волны, которая, по сути, является скоростью распространения упругих деформаций жидкости в трубе.

Здесь первое слагаемое под корнем характеризует упругие свойства рабочей среды (жидкости), а – второе упругие силы материала трубы.

Рассмотрим подробнее эти слагаемые.

Как известно из гидростатики, сила, действующая на цилиндрическую поверхность, равна произведению давления на проекцию площади этой поверхности в направлении действия силы. На рассматриваемый участок трубы с толщиной стенок ?, длиной L и диаметром D действует изнутри давление P. Вследствие этого возникает разрывающая сила F, равная

.

В стенках трубы возникает сила сопротивления

, равная произведению площади сечения стенок трубы

на внутренние напряжения

в материале стенок трубы, т.е.

.

Если приравнять две эти силы, получим равенство

,

из которого найдём выражение, определяющее внутреннее напряжение в стенках трубы

Полагая, что относительное увеличение диаметра трубы, равное

, прямо пропорционально напряжению в стенках трубы, можно записать

где Ет - коэффициент пропорциональности, который является модулем упругости материала трубы.

Из двух последних выражений следует, что абсолютное приращение радиуса сечения трубы может быть выражено формулой

Запишем выражение, определяющее увеличение площади сечения трубы:

где ? – начальная площадь сечения трубы,

?р – площадь сечения трубы при давлении P.

Пренебрегая малой величиной высшего порядка ?R2 и подставив выражение для ?R, получим

Продифференцировав это выражение по P и рассматривая ? как функцию, зависящую от P, получим:

В итоге слагаемое, описывающее упругие свойства материала трубы в выражении для скорости распространения ударной волны, можно представить в следующем виде:

Теперь рассмотрим слагаемое, описывающее упругость жидкости

. Ранее при рассмотрении свойств жидкости было установлено, что если изменение объёма происходит за счёт изменения плотности, то можно определить коэффициент сжимаемости жидкости ?w:

Часто этот коэффициент выражают через обратную величину, называемую модулем упругости жидкости Eж, т. е.:

Отсюда следует, что второе слагаемое, характеризующее упругие свойства рабочей среды, может быть представлено в виде:

Таким образом, окончательно выражение для скорости распространения ударной волны в упругом трубопроводе можно переписать в следующем виде:

где

- плотность жидкости,

D - диаметр трубопровода,

- толщина стенки трубопровода,

Ет – объёмный модуль упругости материала трубы,

Еж - объёмный модуль упругости жидкости.

Из формулы следует, что скорость распространения ударной волны зависит от сжимаемости жидкости и упругих деформаций материала трубопровода.

Содержание раздела